前言

昨天先教學了 Heap 的基本定義、部分操作，也先複習了 Complete BT 的概念來幫助理解 Heap，今天要進入的部分就是如何建立一個 Heap

Build a Heap Operation

在建立一個 Heap 的時候，可以選擇採用

1. Top-Down 方法：時間複雜度為 O(nlogn)
2. Bottom-Up 方法：時間複雜度為 O(n)

Top-Down 方法

即為一個一個元素插入 Heap 並進行調整
可以先簡單的分析一下 Top-Down 方法的時間複雜度，依照昨天所說著插入一個點進入 Heap，由於每插入一點就必須挑戰父點直到不能挑戰或挑戰到 root，因此每插入一次至多就會調整最小樹高的次數，就會是 O(logn)，假設目前建立 Heap 時，每次都進行至多次數的調整，會得到以下算式

因此利用 Top-Down 法之時間複雜度為 O(nlogn)

Bottom-Up 方法

1. 先將所有元素置入 Array
2. 再從最後一個父點開始調整直到root
   演算法如下

// 由 1.adjust(tree,i,n) 即 heapify 2.buildHeap(tree,n) 所組成

adjust(tree,i,n){ //i為parent index
	x = tree[i];
	j = 2*i; // 左子點的index 
	while(j<=n){ // 還有子點
		if(j<n) // 還有右兄 n is last node index & total numbers
			if(tree[j] < tree[j+1]) j=j+1; // 如果右兄比較大就要拿右兄來換
		if(x > tree[j]) break; // 如果 x 比較大就不用調整
		else{
				swap(tree,j/2,j);		
		}
		j*=2;
	}
}

buildHeap(tree,n){
	for(int i=n/2;i>0;i--){ // n/2 為 last parent
		adjust(tree,i,n);
	}
}

而我們可以觀察一下下面 Complete BT，樹高為 log(n+1) ，假設父點位於 Level i，從此父點調整子樹為 Heap，最大移動成本為 k-i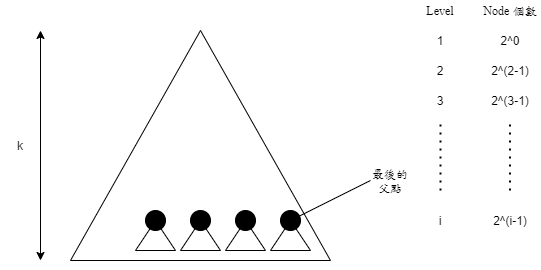

接著觀察每 Level 的 Node 個數，代表有多少父點的子樹要調整，所以為 2^(i-1) 個
所以我們可以從 Level 1~k 去計算調整次數

令此式為 S，可以使用雙邊乘上 2 去解可以得到 k=2n-logn-2 因此時間複雜度為 O(n)，表現比 Top-Down 法好，因此常使用 Bottom-up 法去建立 Heap